- Identifica el numerador y el denominador de la fracción que deseas simplificar. Por ejemplo, si tienes la fracción 8/12, el numerador es 8 y el denominador es 12.
- Busca el número máximo que divide al numerador y al denominador sin dejar residuo. Este número se llama el factor común. En el ejemplo anterior, el factor común es 4, ya que 4 divide tanto a 8 como a 12 sin dejar residuo.
- Divide tanto el numerador como el denominador por el factor común identificado en el paso anterior. En el ejemplo, 8/12 se divide por 4 para obtener 2/3.
- Verifica si la fracción puede simplificarse aún más. Si el numerador y el denominador tienen factores comunes adicionales, repite los pasos 2 y 3 hasta que la fracción no se pueda simplificar más.
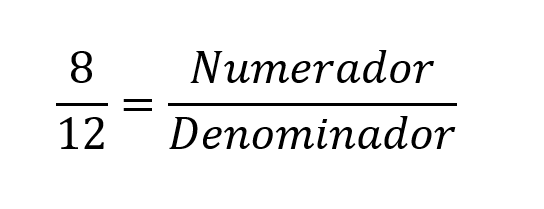
El factor común es el número más grande que divide al numerador y al denominador de una fracción sin dejar residuo. Por ejemplo, en la fracción 8/12, el factor común más grande es 4, ya que 4 divide tanto a 8 como a 12 sin dejar residuo. Una vez que se ha encontrado el factor común, es posible reducir la fracción dividiendo tanto el numerador como el denominador por este factor. En el ejemplo anterior, dividiendo el numerador y el denominador por 4 se obtiene la fracción simplificada 2/3.
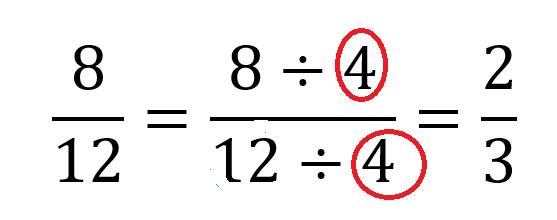
Por lo tanto, la fracción 8/12 se puede simplificar a 2/3. Si el resultado de la fracción no es un número entero, recuerda que los profesores suelen pedir que los resultados se simplifiquen tanto como sea posible.
Ejemplos:
- Simplificar la fracción 10/25: Identificamos el factor común de 10 y 25, que es 5. Dividimos tanto el numerador como el denominador por 5, obteniendo la fracción 2/5.
- Simplificar la fracción 18/24: Identificamos el factor común de 18 y 24, que es 6. Dividimos tanto el numerador como el denominador por 6, obteniendo la fracción 3/4.
- Simplificar la fracción 9/36: Identificamos el factor común de 9 y 36, que es 9. Dividimos tanto el numerador como el denominador por 9, obteniendo la fracción 1/4.
Otro método
Otro método para simplificar fracciones es utilizando el máximo común divisor (MCD) entre el numerador y denominador.
Para utilizar este método, se deben seguir los siguientes pasos:
- Encontrar el MCD del numerador y denominador.
- Dividir ambos términos de la fracción por el MCD.
- La fracción resultante será la forma simplificada de la fracción original.
Por ejemplo, si queremos simplificar la fracción 24/36, se debe encontrar el MCD de 24 y 36, que es 12. Luego, se divide tanto el numerador como el denominador entre 12, lo que resulta en la fracción simplificada de 2/3.
Es importante mencionar que la simplificación de fracciones es útil para realizar cálculos más sencillos y presentar resultados de manera más clara y ordenada.
Para encontrar el máximo común divisor (MCD) de dos o más números usando el método de la tabla, se pueden seguir los siguientes pasos:
- Escribir los números que se quieren calcular en la parte superior de una tabla.
- En la primera columna de la tabla, escribir los factores primos de cada número.
- Identificar los factores primos comunes de los números y escribirlos en la segunda columna de la tabla.
- Multiplicar los factores primos comunes en la segunda columna de la tabla.
- Repetir los pasos 3 y 4 hasta que no haya más factores primos comunes.
- El producto de los factores primos comunes es el MCD de los números.
A continuación, se muestra un ejemplo de cómo se puede utilizar el método de la tabla para encontrar el MCD de los números 24 y 36:
| Números | Factores primos | Factores primos comunes |
| 24 | 2 x 2 x 2 x 3 | 2 x 2 x 3 |
| 36 | 2 x 2 x 3 x 3 | 2 x 2 x 3 |
| 2 x 2 x 3 = 12 | ||
| Números | Factores primos | Factores primos comunes |
| 24 | 2 x 2 x 2 x 3 | 2 x 2 x 3 |
| 36 | 2 x 2 x 3 x 3 | 2 x 2 x 3 |
| No comunes | 2 x 2 x 3 = 12 |
En este ejemplo, los factores primos comunes son 2, 2 y 3. Al multiplicarlos, se obtiene el valor de 12, que es el MCD de los números 24 y 36.
El estudiante tiene la opción de elegir el método que más le guste para resolver un problema matemático. Cada método tiene sus ventajas y desventajas, y algunos pueden ser más adecuados para ciertos tipos de problemas. Es importante que los estudiantes experimenten con diferentes métodos y encuentren el que mejor se adapte a sus necesidades y estilo de aprendizaje. Al tener la flexibilidad de elegir el método que prefieran, los estudiantes pueden desarrollar su pensamiento crítico y mejorar su capacidad para resolver problemas de manera eficiente y efectiva.